Ngành Toán học
Trình độ đào tạo:
Thời gian đào tạo
MỤC TIÊU ĐÀO TẠO
- Đào tạo cử nhân Toán học có năng lực chuyên môn, phẩm chất chính trị, đạo đức và sức khỏe tốt.
Trang bị những kiến thức đại cương về khoa học xã hội và nhân văn, về khoa học tự nhiên, cũng như những kiến thức cơ bản về toán học cho sinh viên nhằm đào tạo họ thành những nhà khoa học chuyên sâu về toán hoặc có khả năng ứng dụng toán vào các lĩnh vực khoa học, công nghệ, kinh tế, xã hội.
- Chương trình hướng tới việc rèn luyện cho sinh viên tư duy chính xác của toán học, tư duy thuật toán, phương pháp tiếp cận khoa học tới các vấn đề thực tế.
- Sinh viên sau khi tốt nghiệp có thể làm công tác giảng dạy tại các trường đại học, cao đẳng, trung học chuyên nghiệp, dạy nghề và trung học phổ thông, hoặc làm việc tại các viện nghiên cứu, các cơ quan quản lý, các cơ sở sản xuất và kinh doanh có sử dụng kiến thức toán học, hoặc nếu có đủ điều kiện có thể được đào tạo tiếp ở các trình độ Thạc sĩ, Tiến sĩ.
CHƯƠNG TRÌNH ĐÀO TẠO
Danh mục các học phần bắt buộc
Kiến thức giáo dục đại cương
1
Triết học Mác-Lênin
9
Tin học cơ sở
2
Kinh tế chính trị Mác-Lênin
10
Đại số và Hình học Giải tích 1
3
Chủ nghĩa xã hội khoa học
11
Đại số và Hình học Giải tích 2
4
Lịch sử Đảng Cộng sản Việt
12
Giải tích 1
5
Tư tưởng Hồ Chí Minh
13
Giải tích 2
6
Ngoại ngữ
14
Cơ học lý thuyết
7
Giáo dục Thể chất
15
Vật lí đại cương
8
Giáo dục Quốc phòng
Kiến thức ngành:
1
Giải tích 3
6
Đại số đại cương
2
Giải tích số
7
Giải tích hàm
3
Phương trình vi phân
8
Lý thuyết độ đo và tích phân
4
Xác suất
9
Hàm biến phức
5
Thống kê toán học
Nội dung một số học phần bắt buộc (phần kiến thức ngành)
Tin học cơ sở
Trang bị cho sinh viên những kiến thức cơ bản nhất về máy tính (thông tin và xử lý thông tin, đại cương về máy tính điện tử, ngôn ngữ của máy tính và hệ điều hành, thuật toán, ngôn ngữ lập trình và chương trình dịch, tổng quan về mạng máy tính và Internet); kỹ năng sử dụng máy tính (hệ điều hành MS DOS, hệ điều hành Windows); ngôn ngữ lập trình Pascal.
Đại số và Hình học Giải tích 1
Cung cấp cho sinh viên những kiến thức cơ bản về phép biểu diễn các đại lượng, các đường, mặt và mối liên hệ giữa chúng bằng các kí hiệu, ma trận, vectơ, phương trình. Nội dung bao gồm: tập hợp, quan hệ, trường số thực, đa thức, phân thức, không gian vectơ, ánh xạ tuyến tính và ma trận, định thức và hệ phương trình đại số tuyến tính.
Trang bị kiến thức về giá trị riêng, vectơ riêng của các đồng cấu, dạng song tuyến tính và dạng toàn phương, không gian vectơ
Giải tích 1
Trang bị cho sinh viên những kiến thức cơ bản về số thực, giới hạn, tính liên tục của hàm một biến, phép tính vi phân và tích phân của hàm một biến.
Giải tích 2
Trang bị những kiến thức về giới hạn, tính liên tục và phép tính vi phân của hàm nhiều biến cũng như chuỗi số, dãy hàm, chuỗi hàm.
Cơ học lý thuyết
Trang bị cho sinh viên những kiến thức cơ bản của Cơ học lý thuyết: Động học và động lực học của chất điểm; Hệ chất điểm và vật rắn; Nhập môn Cơ học giải tích: các nguyên lý độ dời khả dĩ, D’Alembert-Euler-Lagrange,
Vật lý đại cương
Trang bị cho sinh viên các kiến thức về nhiệt học, điện học, quang học: các nguyên lý trong nhiệt động lực học; các khái niệm cơ bản như nhiệt độ, nội năng, công, năng lượng; điện trường trong chân không; vật dẫn trong điện trường; năng lượng của điện trường; dòng điện không đổi; dòng điện trong môi trường; từ trường trong chân không; chuyển động của hạt tích điện trong điện trường; từ trường; cảm ứng điện từ; cơ sở của lý thuyết Maxwell với trường điện từ.
Giải tích 3
Cung cấp kiến thức về tích phân phụ thuộc tham số, tích phân bội, tích phân đường, tích phân mặt cũng như mối liên hệ giữa tích phân đường, tích phân mặt với tích phân bội.
Trong tổng số thời lượng bài tập của các học phần Giải tích 1,2,3 dành 10 tiết để giới thiệu một phần mềm tính toán (Mapple, Mathematica, vv...).
Giải tích số
Trang bị cho sinh viên những kiến thức cơ bản về lý thuyết xấp xỉ hàm và giải gần đúng các phương trình, bao gồm các nội dung sau: phép nội suy, xấp xỉ đều, xấp xỉ trung bình phương, ứng dụng của lý thuyết xấp xỉ để tính gần đúng đạo hàm và tích phân, giải gần đúng phương trình siêu việt, giải hệ phương trình đại số tuyến tính, tìm giá trị riêng, vectơ riêng của ma trận, giải gần đúng bài toán giá trị ban đầu và bài toán biên hai điểm cho phương trình vi phân thường.
Phương trình vi phân
Cung cấp kiến thức về các phương pháp giải tích để tìm nghiệm cũng như các tính chất và dáng điệu nghiệm: Phương trình vi phân cấp 1, cấp 2, và cấp cao; Định thức Vronski, hệ nghiệm cơ bản, công thức Ostrogradski-Liouville, phương pháp biến thiên hằng số; Lý thuyết tổng quát về hệ phương trình tuyến tính; Sự ổn định nghiệm của hệ phương trình vi phân tuyến tính; Sự ổn định theo xấp xỉ thứ nhất.
Xác suất
Cung cấp các kiến thức cơ bản về xác suất: biến cố, xác suất của biến cố, các tính chất của xác suất; đại lượng ngẫu nhiên rời rạc và đại lượng ngẫu nhiên liên tục; các đặc trưng của đại lượng ngẫu nhiên: kỳ vọng, phương sai; các loại phân phối cơ bản: phân phối nhị thức, Poisson, mũ, chuẩn, đều, ...; vectơ ngẫu nhiên và phân phối của vectơ ngẫu nhiên; luật số lớn và các định lý giới hạn.
Thống kê toán học
Trình bày mô hình thống kê, khái niệm và các ví dụ; lý thuyết ước lượng: ước lượng điểm, ước lượng khoảng không chệch cho các đặc trưng của đại lượng ngẫu nhiên; các phương pháp ước lượng cơ bản (phương pháp bình phương tối thiểu, phương pháp mômen, phương pháp hợp lý cực đại, phương pháp Bayes, lý thuyết kiểm định giả thiết).
Đại số đại cương
Trang bị cho sinh viên những kiến thức cơ bản về các cấu trúc quan trọng của đại số trừu tượng: nhóm, vành, trường, đa thức, môđun và đại số, đại số Bool.
Giải tích hàm
Cung cấp những kiến thức cơ bản về không gian và toán tử, bao gồm: không gian metric, không gian tuyến tính định chuẩn, không gian có tích vô hướng, toán tử tuyến tính, định lý ánh xạ mở, đồ thị đóng, nguyên lý bị chặn đều, phổ của toán tử compact tự liên hợp, định lý Fredholm. Sơ lược về phép tính vi phân trong không gian tuyến tính định chuẩn.
Lý thuyết độ đo và tích phân
Trình bày lý thuyết độ đo Lebesgue, tích phân Lebesgue, độ đo tích và định lý Fubini, độ đo suy rộng, định lý Radon-Nykodim, định lý phân tích Lebesgue.
Hàm biến phức
Trang bị cho sinh viên kiến thức cơ bản về: Hàm chỉnh hình và ánh xạ bảo giác (mặt phẳng phức và hàm biến phức, hàm chỉnh hình, ánh xạ bảo giác); Hàm chỉnh hình và thặng dư (các tính chất cơ bản của hàm chỉnh hình, thặng dư và ứng dụng).
ĐỪNG BỎ QUA BÀI VIẾT BÊN DƯỚI:
X3 doanh số thực chiến không màu mè, đọc là làm luôn!
Top 13 Công Cụ Tìm Kiếm Hottrend Để Tăng Tương Tác
Top 48 Công Cụ Nghiên Cứu Từ Khóa Tốt Nhất
7 Quy Tắc Tối Ưu Fanpage Chuẩn Seo
Hướng Dẫn Tạo Nhóm Facebook Trăm Nghìn Thành Viên Từ A-Z
Tin Thông tin tuyển sinh khác

Tra Cứu Điểm Thi Tốt Nghiệp Thpt 2012
Diemtuyensinh.com - Tra Cứu Điểm Thi Tốt Nghiệp Thpt 2012 22:08 23/06/2025
ĐH Y Dược TP.HCM tuyển sinh đào tạo Sau đại học năm 2023
Điểm Tuyển Sinh - ĐH Y Dược TP.HCM tuyển sinh đào tạo Sau đại học năm... 17:48 13/09/2023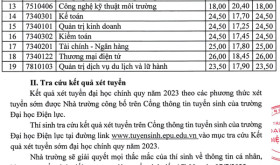
Điểm Chuẩn Trúng Tuyển Năm 2023 Theo Các Phương Thức Xét Tuyển Sớm Của Trường Đh Điện Lực
Diemtuyensinh.com - Điểm Chuẩn Trúng Tuyển Năm 2023 Theo Các Phương Thức Xét Tuyển Sớm Của Trường... 15:52 20/06/2025
Ngành Nông Học
Diemtuyensinh.com - Ngành Nông Học 17:04 21/06/2025
Ngành Quốc Phòng
Diemtuyensinh.com - Ngành Quốc Phòng 16:52 21/06/2025
Chỉ Tiêu Tuyển Sinh Lớp 10 Của Các Trường Tư Thục Năm Học 2023-2024 Tại Hà Nội
Diemtuyensinh.com - Chỉ Tiêu Tuyển Sinh Lớp 10 Của Các Trường Tư Thục Năm Học 2023-2024 Tại Hà... 13:32 20/06/2025
Ngành Khai Thác Dầu Khí
Diemtuyensinh.com - Ngành Khai Thác Dầu Khí 18:37 21/06/2025
Ngành Công Nghệ Hóa Học
Diemtuyensinh.com - Ngành Công Nghệ Hóa Học 16:46 21/06/2025
Thi THPT quốc gia: Thí sinh vẫn chuộng khối ngành kinh tế
Theo số liệu thống kê của Bộ GD-ĐT, chỉ tính riêng số thí sinh đăng ký xét tuyển nguyện vọng 1... 11:29 02/08/2023
Điểm Chuẩn 2014: Trường Đh Quốc Tế Miền Đông
Diemtuyensinh.com - Điểm Chuẩn 2014: Trường Đh Quốc Tế Miền Đông 16:01 20/06/2025ĐƯỢC QUAN TÂM NHIỀU
 Đề thi và đáp án môn Ngữ Văn thi tốt nghiệp THPT 2025 (tham khảo)
Thông tin Điểm Tuyển Sinh cập nhật đề thi kết quả đáp án môn Ngữ Văn kỳ thi tốt nghiệp THPT 2025...
Đề thi và đáp án môn Ngữ Văn thi tốt nghiệp THPT 2025 (tham khảo)
Thông tin Điểm Tuyển Sinh cập nhật đề thi kết quả đáp án môn Ngữ Văn kỳ thi tốt nghiệp THPT 2025...
 ĐH Y Dược TP.HCM tuyển sinh đào tạo Sau đại học năm 2023
ĐH Y Dược TP.HCM tuyển sinh đào tạo Sau đại học năm 2023
 Trước khi đăng ký dự thi tốt nghiệp THPT 2024, thí sinh cần chuẩn bị giấy tờ gì?
Trước khi đăng ký dự thi tốt nghiệp THPT 2024, thí sinh cần chuẩn bị giấy tờ gì?
 Danh sách các trường nhận xét tuyển học bạ trong tháng 4/2024
Danh sách các trường nhận xét tuyển học bạ trong tháng 4/2024
 Trường Cao đẳng Sài Gòn
Trường Cao đẳng Sài Gòn
 Chuẩn đầu ra tiếng Anh của các trường Đại học hiện nay
Chuẩn đầu ra tiếng Anh của các trường Đại học hiện nay
 Trường Cao đẳng Tài chính Hải quan
Trường Cao đẳng Tài chính Hải quan
BÀI VIẾT MỚI CẬP NHẬT
 Tra Cứu Điểm Thi Tốt Nghiệp Thpt 2012
Diemtuyensinh.com - Tra Cứu Điểm Thi Tốt Nghiệp Thpt 2012
Tra Cứu Điểm Thi Tốt Nghiệp Thpt 2012
Diemtuyensinh.com - Tra Cứu Điểm Thi Tốt Nghiệp Thpt 2012
 Trường Trung cấp Cơ điện Nam Định
Trường Trung cấp Cơ điện Nam Định
 Trường Trung cấp nghề Việt - Hàn Bình Dương
Trường Trung cấp nghề Việt - Hàn Bình Dương
 ĐH Y Dược TP.HCM tuyển sinh đào tạo Sau đại học năm 2023
ĐH Y Dược TP.HCM tuyển sinh đào tạo Sau đại học năm 2023
 Đáp án môn Sinh Học kỳ thi tốt nghiệp THPT 2025 full 48 mã đề (tham khảo)
Đáp án môn Sinh Học kỳ thi tốt nghiệp THPT 2025 full 48 mã đề (tham khảo)
 Đáp án môn Tin học kỳ thi THPT 2025 Full mã đề (tham khảo)
Đáp án môn Tin học kỳ thi THPT 2025 Full mã đề (tham khảo)
 Đáp án môn Công nghệ Nông nghiệp kỳ thi THPT 2025 full mã đề (tham khảo)
Đáp án môn Công nghệ Nông nghiệp kỳ thi THPT 2025 full mã đề (tham khảo)
TUYỂN SINH THEO KHU VỰC
 Các trường Quân đội - Công An
Các trường Quân đội - Công An
 Các trường Đại học - Học viện khu vực TP.HCM
Các trường Đại học - Học viện khu vực TP.HCM
 Các trường Đại học - Học viện khu vực Hà Nội
Các trường Đại học - Học viện khu vực Hà Nội
 Các trường Trung cấp khu vực miền Bắc
Các trường Trung cấp khu vực miền Bắc
 Các trường Trung cấp tại khu vực TP. Hồ Chí Minh
Các trường Trung cấp tại khu vực TP. Hồ Chí Minh
 Các trường Trung cấp khu vực miền Trung và Tây Nguyên
Các trường Trung cấp khu vực miền Trung và Tây Nguyên
 Các trường Trung cấp khu vực miền Nam
Các trường Trung cấp khu vực miền Nam
 Các trường Trung cấp khu vực TP. Hà Nội
Các trường Trung cấp khu vực TP. Hà Nội
 Các trường Cao đẳng khu vực TP. Hồ Chí Minh
Các trường Cao đẳng khu vực TP. Hồ Chí Minh
 Các trường Cao đẳng khu vực TP. Hà Nội
Các trường Cao đẳng khu vực TP. Hà Nội
 Các trường Cao đẳng khu vực miền Bắc
Các trường Cao đẳng khu vực miền Bắc
 Các trường Đại học khu vực miền Trung & Tây Nguyên
Các trường Đại học khu vực miền Trung & Tây Nguyên
 Các trường Đại học khu vực miền Nam
Các trường Đại học khu vực miền Nam
 Các trường Đại học khu vực miền Bắc
Các trường Đại học khu vực miền Bắc
 Các trường Cao đẳng khu vực Miền Trung - Tây Nguyên
Các trường Cao đẳng khu vực Miền Trung - Tây Nguyên
 Các trường Cao đẳng khu vực miền Nam
Các trường Cao đẳng khu vực miền Nam
 Các Trường Cao đẳng đào tạo ngành Sư phạm
Các Trường Cao đẳng đào tạo ngành Sư phạm
BÀI VIẾT ĐANG HOT
 Đáp án môn Tin học kỳ thi THPT 2025 Full mã đề (tham khảo)
Thông tin Điểm Tuyển Sinh Cập nhật đáp án môn Tin học kỳ thi THPT 2025 mới nhất được giải bởi các...
Đáp án môn Tin học kỳ thi THPT 2025 Full mã đề (tham khảo)
Thông tin Điểm Tuyển Sinh Cập nhật đáp án môn Tin học kỳ thi THPT 2025 mới nhất được giải bởi các...
 Đáp án môn Công nghệ Nông nghiệp kỳ thi THPT 2025 full mã đề (tham khảo)
Đáp án môn Công nghệ Nông nghiệp kỳ thi THPT 2025 full mã đề (tham khảo)
 Đáp án môn Công nghệ Công nghiệp kỳ thi THPT 2025 full mã đề (tham khảo)
Đáp án môn Công nghệ Công nghiệp kỳ thi THPT 2025 full mã đề (tham khảo)
 Đáp án môn Giáo Dục Kinh Tế và Pháp Luật kỳ thi tốt nghiệp THPT 2025 full 48 mã đề
Đáp án môn Giáo Dục Kinh Tế và Pháp Luật kỳ thi tốt nghiệp THPT 2025 full 48 mã đề
 Đáp án môn Địa Lý kỳ thi tốt nghiệp THPT 2025 full 48 mã đề (tham khảo)
Đáp án môn Địa Lý kỳ thi tốt nghiệp THPT 2025 full 48 mã đề (tham khảo)
 Đáp án môn Hoá kỳ thi tốt nghiệp THPT 2025 full 48 mã đề (tham khảo)
Đáp án môn Hoá kỳ thi tốt nghiệp THPT 2025 full 48 mã đề (tham khảo)
 Đề thi và đáp án môn Toán thi tốt nghiệp THPT 2025 (tham khảo)
Đề thi và đáp án môn Toán thi tốt nghiệp THPT 2025 (tham khảo)
Bản quyền 2024 @ Diemtuyensinh.com
Cảm ơn bạn!
Cảm ơn bạn đã hoàn thành form. Hãy nhấn vào liên kết dưới đây để tải tệp:
Tải xuống tệp

